شما نمیدانید چقدر شعر در محاسبهٔ یک جدول لگاریتم وجود دارد.
مقدمه
تا جایی که به خاطر دارم، پدرم همیشه مشکلات شنوایی داشت. به همین دلیل، هر از گاهی مجبور بود آزمایشی به نام «شنوایینگار» (audiogram) انجام دهد. شنویایینگار نموداری شبیه شکل بالاست است.
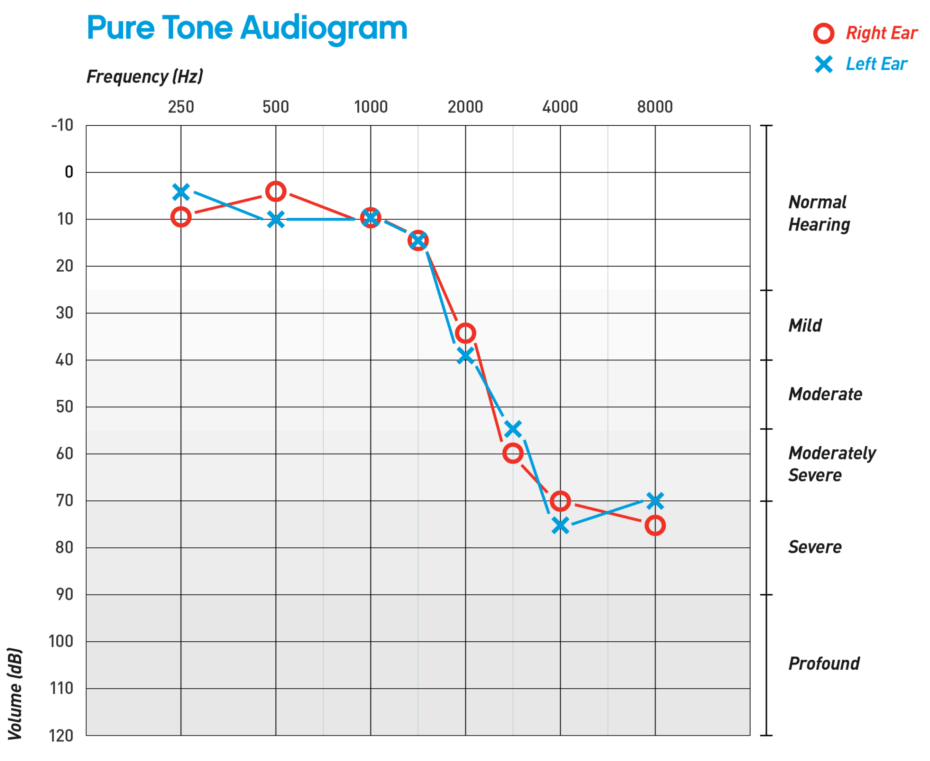
روی محور افقی، فرکانسهایی از ۲۰ تا ۱۰٬۰۰۰ را میبینید (اگرچه انسان میتواند صداهایی تا ۲۰٬۰۰۰ هرتز را هم بشنود). اما محور عمودی سطح شنوایی را در واحدی به نام دسیبل (decibel) نشان میدهد. دسیبل بهطور تحتاللفظی بهمعنای «ده بل (bel)» است، ولی خودِ «بل» یک واحد لگاریتمی است. این بدان معناست که ۴۰ دسیبل در واقع ده برابر قویتر از ۳۰ دسیبل است! اما چرا باید اینطور باشد؟ چرا از واحدی لگاریتمی برای اندازهگیری شنوایی استفاده میکنیم؟ جستجو برای پاسخ به این سؤال ما را به درکی عمیق از لگاریتم، مغز، ادراک و اطلاعات میرساند.
فشنر و پایهگذاری روانفیزیک
گوستاو تئودور فشنر (Gustav Theodor Fechner)، فیزیکدان، فیلسوف و روانشناس آلمانی، بنیانگذار آن چیزی است که امروزه به نام روانفیزیک (psychophysics) شناخته میشود. فشنر رابطهٔ میان تحریکات فیزیکی (physical stimuli) و احساسات یا ادراکات (sensations / perceptions) حاصل از آنها را مورد مطالعه قرار داد. مطالعات او افق جدیدی برای درک ذهن انسان و ارتباط آن با جهان فیزیکی گشود.
فشنر شاگرد فیزیکدان و روانشناس دیگر آلمانی به نام ارنست هاینریش وبر (Ernst Heinrich Weber) بود. وبر مشاهده کرد که «حداقل افزایش در یک محرک که منجر به افزایش قابلدرک در حس میشود، متناسب با اندازهٔ اولیهٔ آن محرک است». برای درک بهتر، به شکل زیر توجه کنید: در هر ستون مربع پایینی ۱۰ نقطه بیشتر از مربع بالایی دارد. اگرچه اختلاف تعداد نقاط در هر دو ستون یکسان است، اما ادراک ما از تفاوت در سمت چپ به وضوح آشکارتر از سمت راست است.
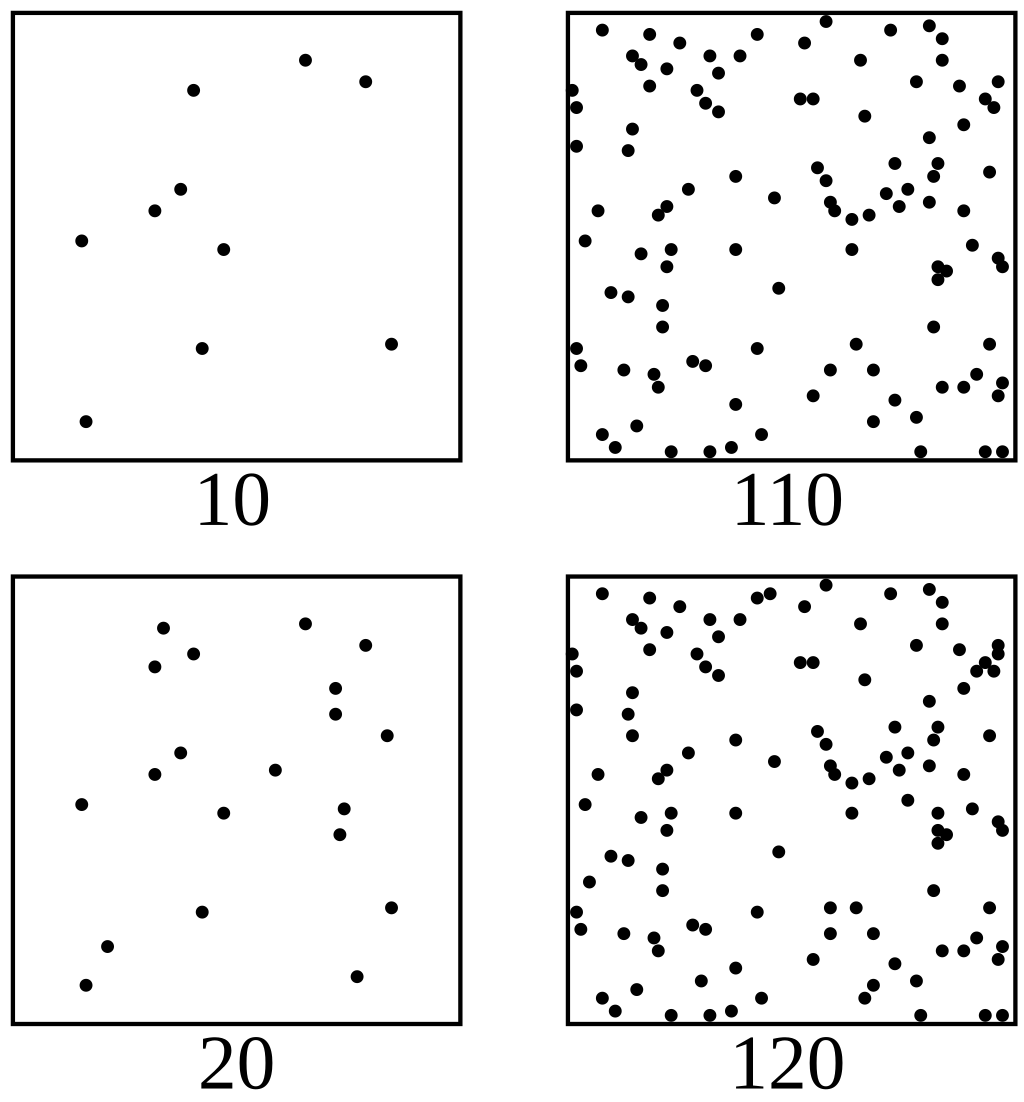
قانون فشنر و رابطه لگاریتمی
در سال ۱۸۶۰، فشنر کتاب مهمی به نام عناصر روانفیزیک (Elemente der Psychophysik) منتشر کرد که در آن به بررسی ایدههای بنیادین دربارهی احساسات انسانی پرداخت. او پیشنهاد داد که تغییرات حسی را بهتر میتوان بهعنوان «تضاد در مقیاس» درک کرد؛ یعنی تشخیص تغییرات بر اساس تفاوتهای نسبی صورت میگیرد، نه مطلق.
فشنر مشاهده کرد که برای آنکه تغییری در یک محرک (مثلاً روشنایی یا وزن) قابل درک باشد، آن تغییر باید نسبت ثابتی از محرک اولیه را تشکیل دهد. به عبارت دیگر:
برای نمونه، اگر وزنهای ۱ کیلوگرمی را به ۲ کیلوگرم افزایش دهیم، فوراً متوجه تغییر میشویم. اما اگر از ۱۰ کیلوگرم به ۱۱ کیلوگرم برویم، همان یک کیلو افزایش بهسختی احساس میشود. برای اینکه تغییری مشابه در سناریوی دوم احساس شود، باید وزن دو برابر شود (از ۱۰ به ۲۰ کیلوگرم تغییر کند). این حداقل تغییر قابل درک، به عنوان تفاوت حداقل قابل احساس (just-noticeable difference یا JND) شناخته میشود.
فشنر نتیجهگیری میکند:
تغییر ادراکی نسبت معکوس با اندازهی اولیهی محرک دارد.
این قانون بهعنوان قانون فشنر (Fechner's Law) شناخته میشود.
فرمولبندی ریاضی
از دیدگاه ریاضی، اگر تغییر کوچکی در ادراک را با dp و محرک را با S نشان دهیم، رابطه به صورت زیر است:
که در آن α یک ثابت تناسب است. اگر از مقدار اولیه S₀ شروع و به S برسیم، کل تغییر خواهد بود:
یا سادهتر:
این رابطه نشان میدهد که نسبت میان تحریکات و ادراکات، یک رابطهٔ لگاریتمی (logarithmic) است. یعنی اگر مقدار محرک چند برابر شود، میزان ادراک فقط بهصورت جمعی (خطی) افزایش مییابد. این اصل محدود به وزن یا شنوایی نیست، بلکه به همهٔ حواس انسانی تعمیم مییابد.
کاربردهای گسترده
برای مثال، سامانهی بینایی ما میتواند روشنایی را در بازهای از صفر تا بیش از ۱۰ به توان ۱۶ برابر تشخیص دهد، اما ادراک ما از روشنایی در این بازه تقریباً خطی افزایش مییابد. در عمل این بدان معناست که بینایی ما از تشخیص حتی یک فوتون (!) تا بیرون رفتن در یک روز آفتابی (۱۰ به توان ۱۶ فوتون) را میتواند مدیریت کند!
به همین شکل، حس چشایی نیز بر اساس مقیاس لگاریتمی کار میکند. زبان به تفاوتهای کوچک در محرکهای ضعیف بسیار حساس است، اما با افزایش شدت، تمایزپذیری کاهش مییابد. برای نمونه، سوکرالوز (sucralose) که یک شیرینکنندهٔ مصنوعی موجود در بسیاری از نوشابههای رژیمی است، تا ۶۰۰ برابر شیرینتر از شکر است، اما ادراک ما از افزایش شیرینی آن نسبتاً اندک است، چرا که ادراک بهصورت لگاریتمی نسبت به شدت محرک افزایش مییابد.
فراتر از حواس پنجگانه
مقیاسبندی لگاریتمی فقط به پنج حس سنتی محدود نمیشود. بلکه شامل ادراک فاصله، زمان و حتی تصمیمگیری نیز میشود. طبق قانون هیک (Hick's Law)، زمانی که افراد برای انتخاب از بین N گزینه صرف میکنند، تنها بهصورت لگاریتمی افزایش مییابد:
این بدان معناست که اگر ده گزینه در برابر شما قرار بگیرد و شما در یک ثانیه تصمیم بگیرید، در برابر ۱۰۰ گزینه این مقدار نه ۱۰ برابر بلکه فقط دوبرابر میشود (رشد خطی).
ادراک مبتنی بر نسبت: بنیان شناخت
انبوهی از پژوهشهای روانشناسی و علوم اعصاب حقیقتی ژرف را آشکار میسازند: ذهن و بدن ما جهان را نه بر اساس مقادیر مطلق، بلکه از طریق نسبتها (ratios) تفسیر میکنند. این ادراک مبتنی بر نسبت (ratio-based perception) چنان عمیق در شناخت ما ریشه دارد که نهتنها بر دیدن و شنیدن و چشیدن، بلکه حتی چارچوب شیوهی اندیشیدن ما نیز شکل میدهد.
ریشهٔ لاتین واژهی logos که به معنای عقل، کلمه، یا نسبت (ratio) است، در قلب این ایده قرار دارد. این واژه بنیانگذار کلماتی چون rationality (خردورزی یا توانایی درک نسبتها و روابط) و logarithm (که معنای تحتاللفظی آن «عددِ نسبت» است) محسوب میشود.
بافتمندی و نسبتگرایی
این جهتگیری بنیادین بهسوی نسبتها، شالودهی بافتمندی (contextuality) را شکل میدهد؛ ویژگیای تعیینکننده در شناخت انسان. ما بهندرت چیزها را در انزوا قضاوت میکنیم؛ بلکه معمولاً آنها را با عناصر پیرامونشان مقایسه میکنیم. یک مطالعه نشان داد که مشتریان یک میکده وقتی موسیقی آلمانی در پسزمینه پخش میشد، با احتمال بسیار بیشتری آبجو آلمانی سفارش میدادند. انتخاب آنها تنها بر اساس ترجیح شخصی نبود، بلکه تحتتأثیر یک نشانه بافتی قرار گرفت؛ یک نسبت بین محیط و انتخاب.
همین اصل توضیح میدهد که چرا یک ساندویچ ۱۰ دلاری در یک غذافروشی سر کوچه گران بهنظر میرسد اما در یک سالن فرودگاهی لوکس ارزان جلوه میکند. یا چرا یک لیوان شراب در صورتیکه به شما بگویند قیمت آن ۱۰۰ دلار است، خوشطعمتر از همان لیوان بهنظر میرسد وقتی بگویند فقط ۱۰ دلار میارزد. در همهٔ این موارد، ارزش در انزوا درک نمیشود، بلکه از جایگاه نسبی آن در یک بافت حسی یا اجتماعی نتیجهگیری میشود.
بستر عصبی نسبتگرایی
در سطح عصبی، این گرایش در حافظهٔ تداعیگر (associative memory) تجلی مییابد. مغز، حقایق را بهصورت جداگانه ذخیره نمیکند؛ بلکه روابط و الگوهای همراهی را بهخاطر میسپارد. این «نسبتهای» درونیشده میان محرکها، اعمال و پیامدها، به ما کمک میکنند تا بهطور مؤثر در جهان حرکت کنیم، شکافها را پر کنیم و بهگونهای انعطافپذیر به موقعیتهای جدید پاسخ دهیم. ما جهان را صرفاً آنگونه که هست نمیبینیم، بلکه آن را در نسبت با سایر چیزها درک میکنیم.
توزیع لگاریتمی-نرمال در مغز
مطالعات اخیر مغز بینشهای ارزشمندی در اینباره ارائه میدهند که چرا هم مغز و هم بدن غالباً بر اساس اصول لگاریتمی عمل میکنند. یکی از نخستین مشاهدات در علوم اعصاب این است که فعالیتهای عصبی از توزیع نرمال (normal distribution یا Gaussian) پیروی نمیکنند. بلکه از توزیع لگاریتمی-نرمال (log-normal distribution) پیروی میکنند: یعنی اکثریت نورونها با فرکانسهای پایین شلیک میکنند، در حالیکه اقلیتی کوچک با نرخهای بسیار بالاتر فعال هستند.
این گروه کوچک از نورونهای با فرکانس بالا که به آنها «انفجارگرهای سریع» (fast burster) گفته میشود، موقعیتی ویژه دارند. آنها نه تنها همواره فعالتر هستند بلکه ارتباطات بیشتری با سایر نورونها برقرار میکنند. این نورونها بهعنوان گرههای مرکزی (hubs) عمل کرده و فعالیت مغز را در قالب یک ساختار شبکهای سلسلهمراتبی (hierarchical network structure) سازمان میدهند که ارتباطات موثر و یکپارچه بین نواحی مختلف مغز را تسهیل میکند.
گیورگی بوشاکی (György Buzsáki) عصبشناس مجارستانی و همکارانش نشان دادهاند که وزنهای سیناپسی (synaptic weights)، اندازهٔ دکمههای آکسونی (axonal bouton sizes)، و نرخ شلیک قشر مغز همگی از توزیعهای سنگیندُم (heavy tail) لگاریتمی-نرمال (log-normal) پیروی میکنند. این موضوع بیانگر فرآیندهای رشد ضربپایهای در مقیاسهای مختلف است. این معماری «پویای لگاریتمی» (log-dynamic) بدین معناست که تعداد کمی گرهٔ بسیار قوی کنترل اصلی شبکه را در دست دارند، در حالیکه بسیاری از ارتباطات ضعیف، انعطافپذیری را فراهم میکنند.
چنین آمارهایی بهطور طبیعی منجر به منحنیهای تقویت (gain curves) مطابق با قانون وبر–فشنر (Weber–Fechner) میشوند: افزایشی متناسب در ورودی پیشسیناپسی، پس از تبدیل به واحدهای لگاریتمی، منجر به تغییری افزایشی در پتانسیل پسسیناپسی میشود. مدلهای محاسباتی نیز تأیید میکنند که وزنهای متمایل و لگاریتمی-نرمال، انتقال اطلاعات را در شرایط محدودیت متابولیکی بهینه میکنند. در بخش بعدی، ریاضیوار نشان خواهیم داد که چرا این انتخاب، «بهینه» است.
محرکهایی که ما را احاطه کردهاند، در بسیاری موارد از قانون توانی (power law) پیروی میکنند، و سامانهٔ شناختی ما برای فشردهسازی دامنهٔ دینامیکی (dynamic-range compression) تطبیق یافتهاست تا انتقال اطلاعات را به شکل بهینه انجام دهد.
فضای اطلاعات: فضایی لگاریتمی
اگر فرض کنیم که اطلاعات در یک فضای احتمالاتی (مثلاً مجموعهای از دادهها با احتمالهایی برای هر بخش) رمزگذاری شده باشد، برای سازماندهی مؤثر این فضا، باید آن را بهصورت مرحلهای و سلسلهمراتبی تقسیم کنیم. این تقسیمبندی مرحلهبهمرحله، چیزی است که در ریاضیات به آن فیلترسازی (filtration) میگویند.
در هر مرحله از این تقسیم، کل فضا به بخشهایی جدا از هم تقسیم میشود. برای مثال: «چاقو» در زیرمجموعه «ابزارهای آشپزخانه» قرار میگیرد، که خود زیرمجموعه «وسایل خانه» است. در هر مرحله، زیرمجموعههای ریزتر داخل یک مجموعه بزرگتر قرار دارند. این ساختار بهصورت یک درخت سلسلهمراتبی (hierarchical tree) دیده میشود.
اگر در هر مرحله تقسیمبندی ثابتی وجود داشته باشد، مثل اینکه هر دسته به ۲ یا ۳ دسته کوچکتر تقسیم شود، تعداد کل بخشها با افزایش مرحلهها بهشکل نمایی رشد میکند. برای شناسایی دقیق یک مورد خاص (مثلاً یک برگ در انتهای درخت)، کافی است تعداد ثابتی سوال چندگزینهای (یا بله/خیر) بپرسیم. این دقیقاً شبیه کارکرد مغز برای فشردهسازی اطلاعات است.
چه چیزی رمزگذاری میشود؟ نسبت بین دستهبندیها
در این ساختار درختی، مهمترین چیزی که ذخیره میشود نسبت بین هر دسته و زیرمجموعههای آن است. مثلاً اگر یک دسته به ۴ بخش تقسیم شود، ممکن است هرکدام سهم خاصی از «احتمال» را به خود اختصاص دهند. این نسبتها اطلاعات اصلی هستند که مغز یا سیستم رمزگذاری نگه میدارد.
هر دادهای که در فضای اطلاعاتی قرار دارد، میتواند با دنبالهای از این نسبتها شناخته شود. در واقع، برای رسیدن به یک نقطه خاص در این فضا، میتوان مسیر را از ریشه درخت تا آن نقطه با دنبالهای از نسبتها (که در بازه ۰ تا ۱ هستند) مشخص کرد. برای درک این موضوع به بازی بیست سوالی دقت کنید: در هر قدم شما به دنبال یافتن سوالی هستید که با نسبت بهتری فضای حالتهای ممکن را تقسیمبندی کند. در اینجا «نسبت» بهینه سوالی است که با جواب دادن به آن به زیربخش کوچکتری از فضا میرسیم به طور مثال اگر طرف مقابل چیزی در ذهن داشته باشد سوال «آیا یک موجود زنده است یا خیر؟» سوال بسیار بهتری است تا «آیا قاشق است؟» چرا که سوال اول تعداد حالتهای بیشتری را حذف میکند!
حالا اگر بهجای ضرب کردن این نسبتها، لگاریتم آنها را بگیریم، عملیات ضرب به جمع تبدیل میشود. این کار باعث میشود تا بتوانیم اطلاعات را بهصورت سادهتر و افزایشی ذخیره کنیم. به همین دلیل، لگاریتم نقشی کلیدی در نحوه پردازش اطلاعات توسط مغز ایفا میکند.
اگر این نسبتها در هر مرحله یکسان باشند، ساختاری شبیه فرکتال (fractal) داریم؛ اما در حالت کلی، هر مرحله میتواند نسبت متفاوتی داشته باشد. در این صورت، فضای اطلاعاتی به یک ساختار چندفرکتالی (multifractal) تبدیل میشود که در آن هر مسیر، ویژگی خاص خود را دارد. برای هر مسیر میتوان عددی به نام «توان هولدر محلی» (local Hölder exponent) تعریف کرد که نشان میدهد چقدر اطلاعات در آن مسیر فشرده یا گسترده شدهاست.
مجموعهای از نقاط که نمای هولدر یکسان دارند، یک «طیف» میسازند که به آن طیف چندفرکتالی (multifractal spectrum) گفته میشود. این طیف به ما کمک میکند تا بفهمیم چگونه اطلاعات در مقیاسهای مختلف توزیع شدهاند.
نتیجهگیری
ما با یک مشاهدهٔ ساده ولی عمیق شروع کردیم: اینکه ادراک ما از جهان خطی نیست، بلکه لگاریتمی است. این واقعیت ساده پیامدهای بزرگی دارد. از آنجا به این نتیجه رسیدیم که این ساختار لگاریتمی فقط ویژگی حواس ما نیست، بلکه یک اصل بنیادی در سازماندهی مغز و هر سیستم شناختی است.
در قلب این ساختار، توانایی شگفتانگیز مغز برای درک جهان از طریق نسبتها قرار دارد؛ چیزی که در نظریهٔ اطلاعات به آن طول کد (code length) میگویند. طول کد لگاریتم تعداد حالتهای ممکن است. این یعنی مغز بهطور طبیعی اطلاعات را فشرده میکند. شناخت یعنی فشردهسازی: یعنی تبدیل سیل ورودیهای حسی به روابط معنادار.
چه در مقایسهٔ صداها، وزنها، روشناییها یا حتی مفاهیم انتزاعی، بدن ما همیشه بهدنبال ساختار از طریق تناسب است. مغز تجربیات وسیع را در قالبهای فشرده و نسبی رمزگذاری میکند. این فقط یک راهبرد نیست؛ این مهراز (معماری) اندیشه است.
در پس هر احساس، هر تصمیم، و هر درک، منطقی عمیق وجود دارد: ذهنی لگاریتمی که جهان را نه آنگونه که هست، بلکه آنگونه که نسبت دارد میبیند و در نهایت، درک کردن یعنی سنجیدن جهان بر اساس نسبتهای آن.
